Full Length Research Article
Local Radiation Dosimetry Method using Optically Stimulated Pulsed Luminescence and Monte Carlo Simulation
Mohammed Talbi1*, M'hamed El Mansouri2, Mounir Ben Messaoud3, Rajaa Sebihi4, Morad Erraoudi4, Yassine Azakhmam4, Mohammed Khalis1
Adv. life sci., vol. 8, no. 2, pp. 160-166, February 2021
*- Corresponding Author: Mohammed Talbi (Email: mo.talbi@uhp.ac.ma)
Authors' Affiliations
2. Ibn Tofail University, faculty of sciences, EPTN, Kenitra – Morocco
3. Sidi Mohamed Ben Abdellah University, Faculty of Sciences Dhar Elmahraz , Fès - Morocco
4. Mohammed V University, faculty of sciences, ESMAR, LHE-SM, Rabat – Morocco
Abstract![]()
Introduction
Methods
Results
Discussion
References
Abstract
Background: This is the first study that has been done in Morocco with the aim of optimizing protection and protocols in diagnostic radiology, by using Monte Carlo simulation and Optically Stimulated Luminescence (OSL).
Methods: Measurements have been performed with solid (AGMS-D+) and OSL detectors to determine the Air Kerma and the backscattering factor on a diagnostic radiology unit.
Results: The spectra simulated by GATE were in a good adequacy with spectra generated by IPEM report 78, with slight differences in the X-rays intensity characteristic, and there was no statistically significant difference between Air Kerma simulated with GATE and those measured using the AGMS-D+ and OSL (P < 0.01).
Conclusion: Monte Carlo simulation responses were suitable and could provide an accurate alternative for Air Kerma and the entrance surface dose determination with non‐uniform primary x‐ray beams.
Keywords: Radiation Dosimetry; Pulsed Luminescence; Monte Carlo Simulation
Diagnostic radiology imaging machines are one of the most widely used man-made radiation sources, and their major task over the years focuses on generating a high quality of the image to well identify the region of interest. However, the achievement of this objective leads to an increase in dose given to the patient. Therefore, understanding the X-ray spectrum is essential for estimating the dose to the patients and for improving image quality [1], the use of computer simulation of X-ray spectra is one of the most important methods used to investigate patient’s dose and image quality. Fewell et al. [2,3] previously performed different target/filter combinations to measure several X-ray spectra. Because of the X-ray spectra measurement difficulties and time consumption, other empirical, semi-empirical, and Monte Carlo modeling methods have been developed for spectra prediction [4,5]. Empirical and semi-empirical models are faster for the X-ray spectra prediction compared to the Monte Carlo modeling methods, but they still have limitations which prevent their adoption for a large range of applications [1,6]. given the limited flexibility, the spectra obtained by these methods do not provide detailed information about the interactions in the target and filters. consequently, this is restricted for the design of new combinations of targets and filters and the optimization of imaging protocols [1,7]. The authors were based on a sophisticated Monte Carlo simulation to overcome the limitations of the mentioned models. Although, Monte Carlo modeling is the slowest and the most computer intensive compared to empirical and semi-empirical methods, it can be applied in systems with different target/filter material composition, and complex geometries. Monte Carlo simulation methods are an important analysis tool for modeling the transport of neutral or charged particles, based upon the probability of distribution for radiation interaction with the matter taking into account all the particles’ geometries and types [8]. There are many codes that were developed such as: MCNP, PENELOPE, BEAMnrc, EGS4, and GEANT4/ GATE [9,10].
The amount of the absorbed and effective dose in diagnostic radiology can be approximated by the incident air Kerma (IAK) due to the low energy of the emitted electrons which will be absorbed locally, though their radiation losses of energy are negligible. Thus, the mass energy transfer and mass energy absorption coefficients are almost identical and the air Kerma is equal to the collision Kerma. The availability of radiation metrology standards directly in terms of water dose for low energy X-ray beams is still scarce [11]. Basic Dosimetry Measurements of diagnostic radiology X-rays are performed primarily in IAK using ICRU74 (ICRU 2006) [12] or IAEA Code of Practice TRS-457 [13] for dosimetry in diagnostic radiology. The transfer of IAK to the entrance surface air Kerma of a phantom (ESAK) requires a correction by the backscattering factor (BSF) and the mass energy–absorption coefficient ratio depend on the field size and on the beam quality.
Furthermore, clinical measurement of IAK does require cost, calibrated equipment and consuming time. Thus, Monte Carlo Simulation remains as an alternative tool on which we can count [11]. Boone et al. [3] recently encouraged researchers to update the coefficients of the computed MC, in the field of radiology because of the technological evolution (beam filtration, potential beam) that radiographic devices have known.
The main objective of this study is to evaluate the Monte Carlo simulation responses of Air KERMA, in the diagnostic radiology field using GEANT4/GATE code. in order to emerge the Monte Carlo simulation as a tool for evaluating Moroccan radiology practices, we proceeded in two steps, we validated the spectra obtained by Gate, based on its comparison with those produced by IPEM-SRS 78 ( semi-empirical model based on a birch and marshal method) [4]. Subsequently, we used two types of detectors: AGMS-D+ and OSL optically stimulated luminescence based on aluminum oxide (Al2O3: C) of small type (nanoDot). to carry out experimental measurements and evaluate the air Kerma obtained by Gate. The two detectors mentioned above have been verified by several studies, and they are used in order to have accurate results [13,14]. Studies have shown that the OSL dosimeters are very sensitive, had a good reproducibility and good linearity [15]. The semiconductor detectors are suitable for clinical applications as described in AIEA TRS 457 [13].
- Experimental measurement
In this study, we have performed numerous manipulations to measure the IAK and the BSF on a conventional General Medical Merate (GMM) radiology system equipped with an X-ray tube model (RTM HS 101), using an AGMS-D+ detector: RADCAL, validated for the energy range of [40 -160kV], and an Accu-Gold multimeter . The result was displayed using the Accu-Gold software: used to display the output parameters and export them to Microsoft Excel format for users. A set of OSL Al2O3 (with 5.0 mm in diameter and 0.2 mm thickness): type NanoDot ™ dosimetry systems (Landauer Inc) were used including a microStar reader [16]. All NanoDots were optically annealed before exposure to clean up previous doses and taking into account background corrections.
IAK measurement: Experimental measurements have been taken to assess the responses of Monte Carlo Air Kerma, by exposing the OSL NanoDot and AGMS-D+-D+ dosimeters, to X-rays from the tube of the GMM industrial radiography unit. The dosimeter was sufficiently above the phantom surface to reduce backscattering and positioned outside the AEC detectors. For each measurement we used a detector identified on the back side of the OSL by a unique alphanumeric code [17].
BSF Estimation: An ABDFAN Phantom was used to evaluate the backscattering factor (anthropomorphic phantom to simulate the patient's abdomen). Prior to calculating the BSF, we measured the Air Kerma at the entrance surface of the phantom ESAK directly using AGMS-D+ and OSL nanoDot dosimeters, they were placed on the ABDFAN phantom surface. Exposure settings have been changed by varying the voltage [50 – 100 kV]. The tube current remained fixed at 70 mAs, and the beam field size was (10*10 cm).We measured with both detectors and we simulated it on the GATE platform. To calculate the backscattering factor, we have used the following equation 1:
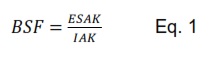
Where BSF is the backscattering factor, ESAK is the Air Kerma at a point on the surface of the phantom, and IAK is the Air Kerma in the free air at the same point without the phantom [18].
- SPECTRAL MODELING BY THE MONTE-CARLO GATE
In general, the spectral modeling methods allow the calculation of numerical values thanks to the computer simulation of pseudo-random numbers, and the reproduction of the various physical phenomena related to particle transport (interactions, energy deposition, emission, etc.). Many simulation codes have been developed for the simulation of low and medium energies’ X-rays such as PENELOPE, MCNP, and GEANT4-GATE [19].
The particle transport simulation method is based on a microscopic modelling; interaction by interaction of the particles’ trajectories followed individually from a series of random numbers and cross sections, and responsible for reproducing the different physical phenomena. The objective behind our interest in spectral simulation is to seek to reproduce the various physical phenomena occurring at the level of X-ray tubes [3].
GEOMETRY OF THE X-RAY TUBE
In order to generate a spectrum of X rays corresponding to the radiology center in RABAT, by taking the conditions used in the experimental measurements: we have modeled an X-ray tube of the RTM HS 101 type from the Monte Carlo simulation platform GATE 7.1 (which is based in particular on a layered architecture embedding the GEANT4 calculation code). We have used a 2.71 CPU i5 laptop. The selected geometrical characteristics are based on the description provided by the manufacture. We notice in the simulations that the filament is modeled by an electron beam which has been defined as a plane source, described by two main characteristics which are its energy and size. Tungsten material with fixed solid angle is used as target (anode). The vacuum prevailing inside the outer shell of the tube has also been modeled. Only the largest field size corresponding to the largest focus 1.2 mm with an angle of 13 degrees was simulated. Amorphous selenium (a-Se) detector materials used for detecting X-ray spectra photon energy. The source to detector distance (SDD) was 24 cm.
- PHYSICAL CONSIDERATIONS OF THE SIMULATION
We started with the definition of a source of electrons, which will be accelerated across a vacuum and which will strike an anode (Tungsten target Z=74) with a density of 18.5 g/cm3. with a fixed angle [20]. We simulated a large number of incident electrons, the energy of the electron beam was 100 KV.
The evolution of secondary particles and the descendants generated by these primary electrons will be tracked, by taking into account the cross sections of the different interactions. We have considered all the physical phenomena that can occur during particle transport (photoelectric effect, multiple, fluorescence after a photoelectric effect, Auger electron ejection, etc.). All the charged particles are then followed in the approximation of a continuous-slowing-down (model that includes positrons, characteristic X-rays, and bremsstrahlung) [7].
For X ray tube used in diagnostic radiology, we produce medium energy photons by braking on targets with high atomic numbers; therefore, the cross section of this effect is not negligible without being at the maximum. This process is responsible for the continuous part of the X-ray spectrum, while taking into account the electronic rearrangement and the photons emission of characteristic energies of transitions, which allows the modeling of the discrete part of the spectrum. For all the activated interactions, the cross sections PENELOPE and STANDARD are both used because they are deemed and more accurate at low energy values. To improve the efficiency of particle transport (electrons and photons), we have used some variance reduction techniques. The first technique fixes the importance of the electron at zero in the regions which have a low contribution to the X-ray spectrum. All the electrons entering these regions will be eliminated in order to save the computation time, the saving time was estimated to be about few hours, and the execution time was 27 hours. The second is for the simulation of the bremsstrahlung phenomenon, which records all the bremsstrahlung photons on a surface outside the X-ray tube. These photons are then fully tracked. This approach consists in improving the efficiency criterion of the code. In addition, the rejection method (RNG) which consists of defining a threshold (in energy or equivalent in distance) for a type of particle in a region of the geometrical space of a given material is also employed [3]. Thus, it was considered that if the particle is not able to leave the current region with an energy greater than the set threshold (until they reach a minimum energy known as energy cut-off by default 1 keV), then its history is over and it gives rise to a local deposit of all of its energy. Finally, some trajectories were also not considered because they were not of interest for the simulation (use of kill boxes). The electron source is described by a rectangular beam of parallel and mono-energetic electrons impacting a surface of the anode.
The geometry of the study is split into two parts: a purely material upper part which does not depend on the presence of an object (patient), and a lower part which concerns the Air Kerma and will therefore depend on the considered object. This approach is called phase space. We proceeded in a similar way, and we have defined a cubic volume at the exit of the X-ray tube. A phase space will be attached to this volume, thus making it possible to record the parameters of all the particles entering this volume for the first time (type, three-dimensional coordinates, direction, energy, production process, weighting, previous interaction volume).
Thanks to this physical modeling, we obtained spectral information that is close to reality, by means of the modeling approximations. The energy spectra have been produced by the implementation of an energy spectrum actor which generate a root document that contains the energy related fluencies.
- SRS-78 SOFTWARE
IPEM has published several versions of the "Catalog of diagnostic X-ray spectra and other data", of which the 1997 software version (report 78) named SRS78 [4]. This software makes it possible to calculate unfiltered spectra from the method of Birch and Marshal [4], and to calculate the IAK per mAs, at 75 cm from the focal point of the tube, for 3 anode materials (tungsten , W; molybdenum, Mo; rhodium, Rh), for different anode slopes (6 to 22 degrees for W, and 9 to 23 degrees for Mo and Rh), and for different filtrations of the tube, depending on the peak value of the high voltage applied to the tube (kVp: from 30 to 150 for W, and 25 to 32 for Mo and Rh) and the generator ripple rate.
SPECTRAL STUDY
To validate the spectrum obtained by the simulation, we compared it with IPEM report 78 which is produced by the introduction of the same X-ray tube configuration. The curves are plotted in the same graph for a reliable comparison Fig1. Quantitative evaluation of the differences between Gate spectra and the spectra generated by IPEM was performed using statistical student’s t-test analysis.
To compare our obtained spectra against IPEM spectra, we normalized the fluencies of the GATE emission spectrum, the results are shown in the Fig1.
The K-edge and L-edge energy peaks obtained in the spectrum generated by GATE, have similar energies of SRS which appear at 58 keV, 60 keV, 69 keV, and 70 keV respectively [1,21]. The K-edge energy peaks are more obvious for IPEM report spectrum than in the simulation results, these results are similar to those reported by Ay et al. [21] using MCNP4C.
the student’s t-test statistical analysis showed there is no statistically significant difference between measured and generated spectrum (p<.05).We noticed from Fig1 that there is a good adequacy of the curves simulated by Gate and those generated by IPEM 78, with slight differences in the characteristic of X-rays intensity. We obtained the same result as Adeli et al. [22]when using the GEANT4 code which showed a lower intensity compared to the IPEM ratio, contrary to what they obtained with the MCNP code.
The characteristic rays generated by IPEM SRS are slightly intense compared to those of our simulation using Gate. Ay et al. [1] reported that IPEM as an empirical method for X-ray spectra using Birch and Marshal model, produce less low energy photons and more high energy photons in the bremsstrahlung X-ray intensity, but in the characteristic intensity all semi-empirical models based on Birch and Marshal model (IPEM, XCOMP and X-raybeam) produce spectra with higher intensity than measured spectra [1].
RADIATION DOSE AIR-KERMA
According to the measurement methodology of international code of practice TRS 457 IAEA [13]. We performed measurements for each tube voltage [50 – 100kV], as shown in Table 1. The tube current remained fixed at 70 mAs, using a field size of 10cm x 10cm and a source-detector distance (SDD) 24 cm.
For a quantitative study, we reproduced the tables obtained by the experimental measurements in the form of graphs and using statistical student’s t-test analysis. Graph (Fig2) shows relationship between Gate IAK and the IAK of the detectors (OSL and AGMS-D+). The Pearson correlation coefficient (r) and the corresponding P values were r=0.997 and (P<.05), consequently no statistically significant difference between IAK simulated with GATE and those measured using the AGMS-D+ and OSL. The Monte Carlo responses are in close linearity with those of the detectors used in the experiments, with a slight difference with the OSL nanoDot detector. The dose-response OSL has previously been reported to be linear for X-rays in the diagnostic energy range [14,19].
The slight difference between Gate results and OSL, it can be explained by the following factors: we have modeled the semiconductor a-Se detector during the simulation GATE, the use of a cardboard holder instead of the probe holder which can affect the detector’s stability, and finally the uncertainty of the measuring instrument. The uncertainty associated with dosimetry measurements in diagnostic radiology depends on numerous factors: Intrinsic error, Field size/field homogeneity, Long term stability of user’s instrument, Air pressure, Temperature and humidity [13].
BACKSCATTERING FACTOR
Using the ESAK and the BSF calculation equation, we found the results in the Fig3, show the backscattering factors (BSF), for monoenergetic photons from the present Monte Carlo simulations for the reference square field sizes 10 * 10 cm.The Pearson correlation coefficient (r) and the corresponding P values were r=0.976 and (P<.05), the BSF calculated by Gate deviates from the measured results by less than 3%.
The backscattering factor first increases with energy and reaches a maximum of 1.31 between 50 and 70kV, afterwards it decreases and reaches a value of 1.19 at 100kV, this is in accordance with the results reported by K. Shimizu et al. [23] and Benmakhlouf et al. 2011 [11], this model is due to a complicated balance between forward and backward scattered Compton photons. In addition, the cross sections for photoelectric absorption and Compton scattering in water intersect at an energy of about 20 keV, comparing with the values of Shimizu and Benmakhlouf, the largest deviation being 12% at around 70 keV lower than Benmakhlouf results and 6,5 % higher than Shimizu result at the same range of energy [11,23].
Figures & Tables
SPECTRAL STUDY
To compare our obtained spectra against IPEM spectra, we normalized the fluencies of the GATE emission spectrum, the results are shown in the figure N°6. The K-edge and L-edge energy peaks obtained in the spectrum generated by GATE, have similar energies of SRS which appear at 58 keV, 60 keV, 69 keV, and 70 keV respectively [1, 22]. The K-edge energy peaks are more obvious for IPEM report spectrum than in the simulation results, these results are similar to those reported by Ay et al. [22] using MCNP4C. the student’s t-test statistical analysis showed there is no statistically significant difference between measured and generated spectrum (p<.05). We noticed from Figure 6 that there is a good adequacy of the curves simulated by Gate and those generated by IPEM 78, with slight differences in the characteristic of X-rays intensity. We obtained the same result as Adeli et al. [23] when using the GEANT4 code which showed a lower intensity compared to the IPEM ratio, contrary to what they obtained with the MCNP code.
The characteristic rays generated by IPEM SRS are slightly intense compared to those of our simulation using Gate. Ay et al. [1] report that IPEM as an empirical method for X-ray spectra using Birch and Marshal model, produce less low energy photons and more high energy photons in the bremsstrahlung X-ray intensity, but in the characteristic intensity all semi-empirical models based on Birch and Marshal model (IPEM, XCOMP and X-raybeam) produce spectra with higher intensity than measured spectra [1].
RADIATION DOSE AIR-KERMA
For a quantitative study, we reproduced the tables obtained by the experimental measurements in the form of graphs and using statistical student’s t-test analysis. Graph (figure5) shows relationship between Gate IAK and the IAK of the detectors (OSL and AGMS-D+). The Pearson correlation coefficient (r) and the corresponding P values were r=0.997 and (P<.05), consequently no statistically significant difference between IAK simulated with GATE and those measured using the AGMS-D+ and OSL. The Monte Carlo responses are in close linearity with those of the detectors used in the experiments, with a slight difference with the OSL nanoDot detector. The dose-response OSL has previously been reported to be linear for X-rays in the diagnostic energy range.
The slight difference between Gate results and OSL, it can be explained by the following factors: we have modeled the semiconductor a-Se detector during the simulation GATE, the use of a cardboard holder instead of the probe holder which can affect the detector’s stability, and finally the uncertainty of the measuring instrument. The uncertainty associated with dosimetry measurements in diagnostic radiology depends on numerous factors: Intrinsic error, Field size/field homogeneity, Long term stability of user’s instrument, Air pressure, Temperature and humidity [13].
BACKSCATTERING FACTOR
Using the ESAK and the BSF calculation equation, we found the results in the Figure 3, show the backscattering factors (BSF), for monoenergetic photons from the present Monte Carlo simulations for the reference square field sizes 10 * 10 cm.The Pearson correlation coefficient (r) and the corresponding P values were r=0.976 and (P<.05), the BSF calculated by Gate deviates from the measured results by less than 3%.
The backscattering factor first increases with energy and reaches a maximum of 1.31 between 50 and 70kV, afterwards it decreases and reaches a value of 1.19 at 100kV, this is in accordance with the results reported by Benmakhlouf et al. 2011 [11], this model is due to a complicated balance between forward and backward scattered Compton photons. In addition, the cross sections for photoelectric absorption and Compton scattering in water intersect at an energy of about 20 keV, comparing with the values of Shimizu and Benmakhlouf, the largest deviation being 12% at around 70 keV lower than Benmakhlouf results and 6,5% higher than Shimizu result at the same range of energy [11].
Conclusion
We evaluated the MC simulation method for estimating X-ray spectra emitted by a tube and detected the X-ray spectra using dose detector, the simulated spectrum was well suited with IPEM reference spectrum. The Air Kerma were estimated with acceptable uncertainties.
The Monte Carlo simulation can provide an accurate alternative for Air Kerma and the entrance surface dose determination with non‐uniform primary x‐ray beams. which can be useful to find a Dose/Image Quality compromise by saving costs and minimizing errors especially in Morocco where measurement equipments are scarce.
Next step of our research will be to study the adapted estimation of dose to the organ by Monte Carlo simulation in order to optimize diagnostic radiology practice.
Author Contributions
Conception and design of study: M. TALBI, M. KHALIS, R. SEBIHI, M. BEN MESSAOUD.
Acquisition of data: M. TALBI, M. EL MANSOURI, M. ERRAOUDI.
Analysis and/or interpretation of data: M. TALBI, M. KHALIS, M. ERRAOUDI, R. SEBIHI.
Drafting the manuscript: M. TALBI, M. EL MANSOURI, M. BEN MESSAOUD.
Revising the manuscript critically for important intellectual content: M. TALBI, M. KHALIS, R. SEBIHI.
Approval of the version of the manuscript to be published: M. TALBI, M. EL MANSOURI.
Authors declare no conflict of interest in this work.
- Ay MR, Sarkar S, Shahriari M, Sardari D, Zaidi H. Assessment of different computational models for generation of x-ray spectra in diagnostic radiology and mammography 2005. pp. 1660-1675.
- Fewell TR, Shuping RE. Photon energy distribution of some typical diagnostic x-ray beams. Medical Physics, (1977); 4(3): 187-197.
- Boone JM, McNitt-Gray MF, Hernandez AM. Monte Carlo Basics for Radiation Dose Assessment in Diagnostic Radiology. Journal of the American College of Radiology, (2017); 14(6): 793-794.
- Evans S. Catalogue of Diagnostic X-Ray Spectra and Other Data. Journal of Radiological Protection, (1998); 18(1).
- Boone JM, Seibert JA. Monte Carlo simulation of the scattered radiation distribution in diagnostic radiology. Medical Physics, (1988).
- Kramer R, Khoury HJ, Vieira JW. CALDose_X – A software tool for the assessment of organ and tissue absorbed doses, effective dose and cancer risks in diagnostic radiology. Physics in Medicine and Biology, (2008); 53(22): 6437-6459.
- Baek C-h, Lee S-j, Kim D. Diagnostic X-ray Spectra Detection by Monte Carlo Simulation. (2018); 12(3): 289-295.
- Cao J, Jiang CY, Zhao YF, Yang QW, Yin ZJ. A novel X-ray tube spectra reconstruction method based on transmission measurements. Nuclear Science and Techniques, (2016); 27(2).
- Salehi Z, Ya Ali NK, Yusoff AL. X-ray spectra and quality parameters from Monte Carlo simulation and analytical filters. Applied Radiation and Isotopes, (2012); 70(11): 2586-2589.
- Sarrut D, Bardiès M, Boussion N, Freud N, Jan S, et al. (2014) A review of the use and potential of the GATE Monte Carlo simulation code for radiation therapy and dosimetry applications. John Wiley and Sons Ltd.
- Benmakhlouf H, Bouchard H, Fransson A, Andreo P. Backscatter factors and mass energy-absorption coefficient ratios for diagnostic radiology dosimetry. Physics in Medicine and Biology, (2011); 56(22): 7179-7204.
- International Commission on Radiation Units and Measurements (ICRU).
- Iaea TRS457; https://www-pub.iaea.org/MTCD/publications/PDF/TRS457_web.pdf
- Musa Y, Hashim S, Karim MKA, Bakar KA, Ang WC, et al. Response of optically stimulated luminescence dosimeters subjected to X-rays in diagnostic energy range. Journal of Physics: Conference Series, (2017); 851(1): 7-13.
- Musa Y, Hashim S, Ghoshal SK, Ahmad NE, Bradley DA, et al. Effectiveness of Al2O3:C OSL dosimeter towards entrance surface dose measurement in common X-ray diagnostics. Radiation Physics and Chemistry, (2019); 165.
- Musa Y, Hashim S, Khalis M, Karim A. Direct and indirect entrance surface dose measurement in X-ray diagnostics using nanoDot OSL dosimeters: Yahaya Musa et al. J Phys: Conf Ser, (2019); 124812014-12014.
- Takegami K, Hayashi H, Nakagawa K, Okino H, Okazaki T, et al. Measurement method of an exposed dose using the nanoDot dosimeter. European Congress of radiology (EPOS), (2015); (April): 1-16.
- Petoussi-Henss N, Zankl M, Drexler G, Panzer W, Regulla D. Calculation of backscatter factors for diagnostic radiology using Monte Carlo methods. Physics in Medicine and Biology, (1998); 43(8): 2237-2250.
- Adeli R, Pezhman Shirmardi S, Amiri J, Singh VP, Medhat M. Simulation and comparison of radiology X-ray spectra. Journal of Paramedical Sciences, (2015); 6(4): 8-14.
- Tran KA, Truong LTH, Mai NV, Dang PN, Vo DTT. Study on the characteristics of X-ray spectra in imaging diagnosis using Monte Carlo simulations. Journal of the Korean Physical Society, (2016); 69(7): 1168-1174.
- Ay MR, Shahriari M, Sarkar S, Adib M, Zaidi H. Monte Carlo simulation of x-ray spectra in diagnostic radiology and mammography using MCNP4C. Physics in Medicine and Biology, (2004); 49(21): 4897-4917.
- Adeli R, Shirmardi SP, Amiri J, Singh VP, Medhat ME. Simulation and comparison of radiology X-ray spectra by MCNP and GEANT4 codes. Journal of Paramedical Sciences, (2015); 6(4): 8-14.
- Shimizu K, Koshida K, Miyati T. Monte Carlo Simulation Analysis of Backscatter Factor for Low-Energy X-Ray. EGS4 Users' Meeting, KEK Proceedings, (2001); 115-118.
This work is licensed under a Creative Commons Attribution-Non Commercial 4.0 International License. To read the copy of this license please visit: https://creativecommons.org/licenses/by-nc/4.0